読書記録・紹介
もうすぐ初期研修が終わるので、(部分的にも)読んで研修医の万人にオススメと思った本をまとめました。研修の途中で出た新しい本もあるが、概ね1年目から読めると思う。あまりにマニアックな本はカットしたが、まだジャンルに偏りがあるかもしれません。多分忘れてる本もあるので追記します。
救急
症候別。10分後に〇〇の患者さんが来るよ、と言われてから見返すのに丁度いい。最近第2版が出ました。
読み物。早めに読んでおくべし。疫学やエビデンス、動き方がわかりやすくまとめられている。
とても有名な本。個人的にはちょっと経験してから見返した方が頭に入りやすかった。
異常に情報量がある。子供の外傷も載っていてとても参考になった。
腹痛診療に苦手意識があり読んだ。
小児診療に苦手意識がある人は多いと思うが、体型的アプローチから各論までとても参考になる。初期研修医・総合診療医のための 小児科ファーストタッチもオススメ。
ERでの創処置 縫合・治療のスタンダード 原著第4版 ちょっと高いがおすすめ。
あとは、BLS, ACLS, PALS のテキストや、当直医マニュアル、疾患別のマニュアルなど
集中治療
循環とは何か? 虜になる循環の生理学 「原理」から説明してくれる本はなかなかなく、これを読めば一気に集中治療に興味が持てると思う。
Dr.竜馬の病態で考える人工呼吸管理 1年目、上級医たちの人工呼吸器についての会話についていけず悲しかったが、これを読んで呼吸器のモニターを見て提案できることもあった。
ICU/CCUの薬の考え方、使い方 ver.2 なかなか分厚く、気になった分野を開いて読む使い方をした。
ICU思考のつくりかた 外科で初めて、じゃあby systemでカルテ書いてと言われて困ってしまった思い出。最近出た本だが、ICUに関わる機会があるなら初めに読むといいと思う。
時系列で紐解く 有益な輸液の話 最近出た本。少し慣れてから読むと奥深さが感じられる。
内科・病棟管理など
病棟指示と頻用薬の使い方 圧倒的おすすめ。1年目の最初に出会いたかった。診療科に関わらず役立つ知識。
循環器のトビラ 新しめの本。研修医レベルにもわかりやすく各疾患の考え方に触れられる。
抗菌薬の考え方,使い方 ver.5 読み物。なんか〜っぽいからとりあえず〜を入れとこう、からレベルアップできる本。
レジデントのための感染症診療マニュアル 第4版 辞書。各論で気になったことが大体載ってる。総論だけでも先に読むとよいかも。
極論で語る腎臓内科 第2版 血液ガスの読み方や尿所見など手広く勉強になった。
ケースでわかるリウマチ・膠原病診療ハンドブック あまり馴染みがないのに疾患群の鑑別も病態もよくわからなくて困ったときに役立った。ちょっとレベル高め。
誰も教えてくれなかった皮疹の診かた・考えかた 病棟で皮疹をみつけたり、看護師さんに皮疹みてくれと言われる機会はよくある。やっぱり考え方から教えてくれる本は面白い。
ベッドサイドの神経の診かた これを買ってから神経診察が楽しくなった。かなりオススメ。
より理解を深める!体液電解質異常と輸液 慣れてきたら、レベルアップに
検査
CT読影レポート、この画像どう書く? この本を抑えておけば研修医として期待されている読影力は満たせると感じる。初めに読むのに圧倒的おすすめ。
新 胸部画像診断の勘ドコロ 放射線科ローテで買った勘ドコロシリーズ(NEOシリーズもある)。エコー、CT、MRIに触れられている。ここまで読めれば自分で鑑別なども考えられる。
あてて見るだけ! 劇的! 救急エコー塾 FASTや心エコーを含め、専門に関わらず広く役立つ。オススメ。
心電図の読み方パーフェクトマニュアル これ+問題集で心電図検定1級に受かった。とりあえず救急系の心電図の本を勉強して、じゃあ何をもって正常と言ってるんですか?と進むのがよいと思う
マニュアル・ポケットブック系
麻酔科研修チェックノート 改訂第7版 当院では指定されていたが、モニターや手技、科別の管理にも触れられていてかつコンパクト。
ポケット呼吸器診療2023 異常な情報量がポケットに。
臨床研究・統計
僕らはまだ、臨床研究論文の本当の読み方を知らない。 研究してみたい、またこれから論文でエビデンスを学んでいくであろう自分たち初心者にオススメ。
ロスマンの疫学 第2版 あるある: introduction と書いてある割に難し
2021 年振り返り (競プロ視点)
何より,働き始めたことで今までのような時間の使い方ができなくなったのでもう競プロは引退かなと思っていたが,意外にも成果が残せた一年だった.
- 2月
医師国家試験があった.試験の日に opencup があり,discord にいった記憶
- 3月
ARC writer をした.結構面白い問題が作れたと思うので解いてほしい.
- 4月
労働開始
- 5月
AtCoder 赤になった.これを通せばほぼ確実に赤,という状況で提出する瞬間めちゃくちゃ手が震えた.赤になるまでかなり時間がかかったため嬉しかったようなほっとしたような.
- 6月
Google Code Jam round 3 で 22 位に入り final 進出した.終了数秒前に submit したら,discord で sigma さんにえっ satashun 通過してるじゃんと言われて結果を知った.数え上げ本当にありがとう.JOI 春合宿で箸にも棒にもかからなかったことが結構人生のコンプレックスだったので,成仏したような感覚があった.問題のレベルや相性はそんなに上振れした感はなかったので,まだ続けていればチャンスがあるかもしれないと思った.
- 8月
GCJ final があった.テンパってしまったのと多倍長にやられてグダグダな結果になってしまった.オンサイトで出たかったね.有名人たちと会話できて感慨深かった.
仕事が結構体力的&時間的に大変だけど,気分転換レベルでも触っていればまだ強くなれるという感触もあるので,もう少し続けていきたい.現状仕事の勉強といい感じのバランスでやれている気がする.
expander.py スクリプト 自分用
.zshrc に関数を定義 expand-acl a.cpp みたいなのを書くと expanded-a.cpp ができる
expand-acl () { dir_cur=$(pwd) echo "${dir_cur}" dir_acl=path-to-ACL-directory echo "${dir_acl}" dup_file=${dir_acl}/dup-$1 cp $1 ${dup_file} echo "file copied to ${dup_file}" cd ${dir_acl} python3 expander.py ${dup_file} new_file=${dir_cur}/expanded-$1 mv combined.cpp ${new_file} rm ${dup_file} cd ${dir_cur} }
テンプレ作成コマンド作成
実は今まで毎回直前に解いた問題のコードを貼ったり,なければテンプレを探しに行ったりのですが (え?),流石に事故りそうなので .zshrc に関数書いた
ACL あるので atcoder とそれ以外でテンプレ分けてます
prepare_atc 1.cpp するとテンプレが 1.cpp に貼られて,prepare_atc_many {a..f}.cpp とかすると a.cpp, b.cpp, ..., f.cpp ができます
# prepare cp-template prepare_atc () { cp path-to-your-template-file $1 } prepare_gen () { cp path-to-your-template-file $1 } prepare_atc_many () { for x in "${@}" do echo "atcoder_template copied to ${x}" prepare_atc ${x} done } prepare_gen_many () { for x in "${@}" do echo "template copied to ${x}" prepare_gen ${x} done }
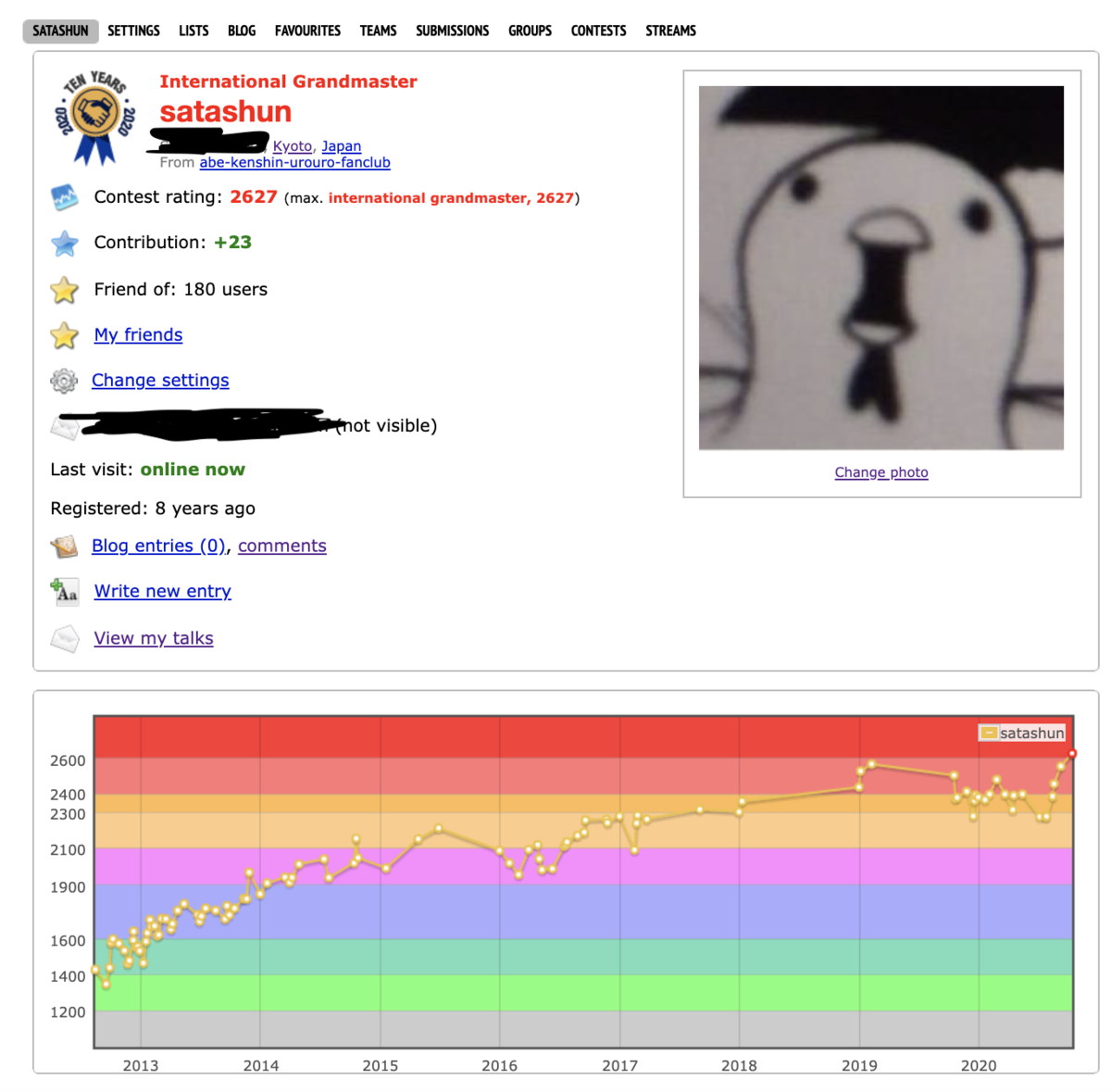
Codeforces で International Grandmaster になった
これは記念記事を残しておくと "達成" したくなくてコンテストに出なくなるのが防げるのではないかという気持ちで書かれた記事です
レートが上がると...嬉しい!
あっとこも 2700 乗ったので頑張りたいね
ARC104 F - Visibility Sequence の別実装例
ネタバレ注意
解説ではボトムアップ (?) に区間を計算していく方法を紹介していましたが、区間を分割していくという視点でも書くことができ、こちらは意識せずとも 4 乗の解法が作れます。
少し数え方の方針が違って、
区間 [l,r] の中で、-1を見ているような一番右のもの、を固定するとそこの値はできるだけ大きくするのが最適です (そのようなものはleft-to-right maxima であって、左も右も条件がゆるくなる) そこで分割すると、左と右の上限が決まります。
よって f(l, r, mx) : 区間 [l, r] を見ていて全ての値が mx 以下、とすると、上述の点ごとに次の左右のmxの値は1つしか遷移しなくていいので単純なメモ化再帰でよいです。